Tensor approach to Markov random fields

A few years ago Oseledets (2011) proposed the Tensor Train decomposition approach. This technique constructs a compact representation of a tensor (multidimensional array) such that allows for efficient application of linear algebra operations. In this project we use the observation that both the energy and the distribution of an MRF with discrete variables can be viewed as tensors. Further, we use the properties of the Tensor Train decomposition to solve some important Markov random field inference problems: the search of the most probable configuration of variables (MAP-inference or energy minimization), estimation of the normalization constant, computing the marginal distributions.

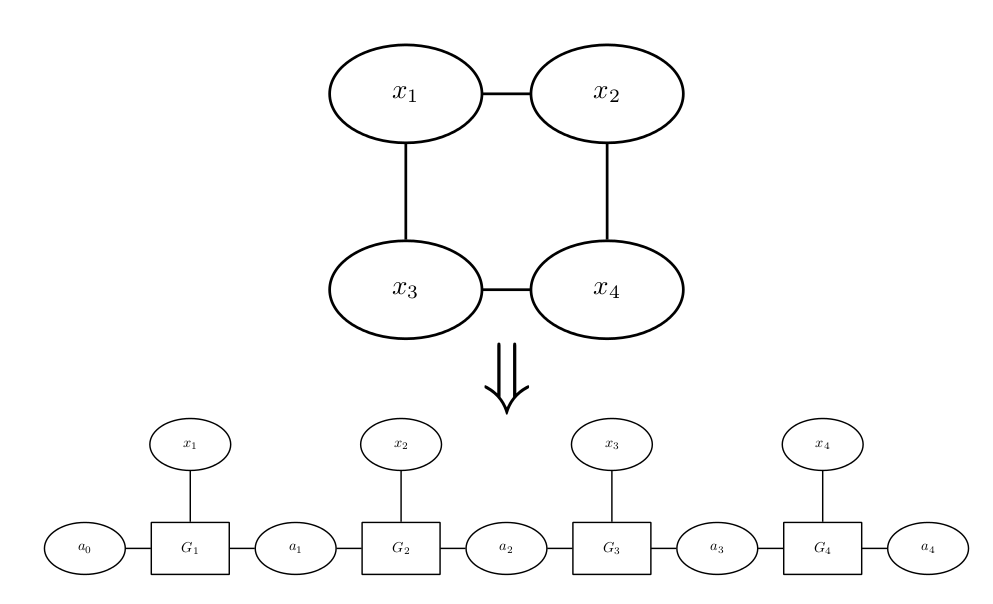
Lots of linear algebra operations for tensors in the Tensor Train format are implemented in the TT-Toolbox. We collaborate with the authors of the Tensor Train decomposition (Scientific Computing group at Skoltech) to develop new application specific algorithms that outperform the current state-of-the-art.

(Oseledets, 2011) Oseledets, I. V. Tensor-Train decomposition. SIAM J. Scientific Computing, 33(5):2295–2317, 2011.

A. Novikov, A. Rodomanov, A. Osokin, D. Vetrov. Putting MRFs on a Tensor Train. Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 2014. JMLR: W&CP volume 32. pdf; supplementary

Talks

1. A. Novikov, A. Rodomanov, A. Osokin, D. Vetrov, Computationally efficient methods for MAP-inference and partition function estimation in MRF in TT format, minisymposium presentation at SIAM Conference on Imaging Science, 2014.

2. A. Rodomanov, A. Novikov, A. Osokin, D. Vetrov, Low-rank approximation of energies in Markov Random Fields and their representation in TT-format, minisymposium presentation at SIAM Conference on Imaging Science, 2014.

3. A. Rodomanov, A. Novikov, A. Osokin, D. Vetrov, Probabilistic graphical models: a tensorial perspective, international conference on Matrix Methods in Mathematics and Applications, 2015.