Variational Optimization in Bayesian Models
Variational methods are known to be effective techniques for solving many optimization and approximation problems and, in particular, for learning in Bayesian models and approximate Bayesian inference. The goal of this project is to apply variational methods for handling Bayesian models consisting of different non-Gaussian components. The main efforts are planned to be made for L1 and L0 regularization.
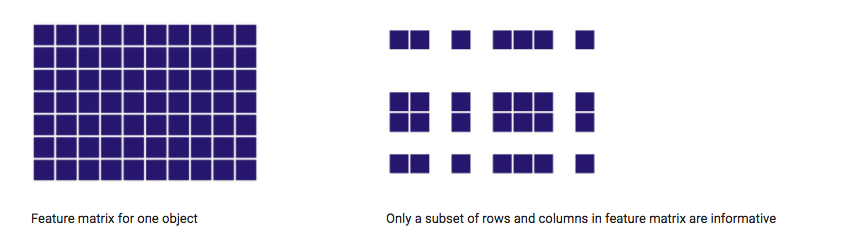
We adopt the Relevance Vector Machine (RVM) framework to handle cases when features are divided into a set of groups (possibly intersected). This is achieved by coupling the regularization coefficients for features’ groups. We present two variants of this new groupRVM framework, based on the way in which the regularization coefficients of the groups are combined. Appropriate variational optimization algorithms are derived for inference within this framework. The consequent reduction in the number of parameters from the initial number of features to the number of features’ groups allows for better performance in the face of small training sets, resulting in improved resistance to overfitting, as well as providing better interpretation of results. We demonstrate the proposed framework for table-structured data such as image blocks and image descriptors when the groups correspond to rows and columns of feature matrix for each object. Experiments are made on synthetic data-sets as well as on a modern and challenging visual identification benchmark.
Group sparsity using ARD approach

We adopt the Relevance Vector Machine (RVM) framework to handle cases when features are divided into a set of groups (possibly intersected). This is achieved by coupling the regularization coefficients for features’ groups. We present two variants of this new groupRVM framework, based on the way in which the regularization coefficients of the groups are combined. Appropriate variational optimization algorithms are derived for inference within this framework. The consequent reduction in the number of parameters from the initial number of features to the number of features’ groups allows for better performance in the face of small training sets, resulting in improved resistance to overfitting, as well as providing better interpretation of results. We demonstrate the proposed framework for table-structured data such as image blocks and image descriptors when the groups correspond to rows and columns of feature matrix for each object. Experiments are made on synthetic data-sets as well as on a modern and challenging visual identification benchmark.
D. Kropotov, D. Vetrov, L. Wolf and T. Hassner. Variational Relevance Vector Machine for Tabular Data. Proceedings of Asian Conference on Machine Learning (ACML) , JMLR Workshop & Conference Proceedings, vol. 13, pp. 79-94, 2010. pdf , link
Have you spotted a typo?
Highlight it, click Ctrl+Enter and send us a message. Thank you for your help!
To be used only for spelling or punctuation mistakes.