Transparent Boundary Conditions

Here we present some results of the work related to construction of boundary conditions that imitate Cauchy problem (ICP).

1. Crank - Nicolson approximation of rod transverse vibration equation. 

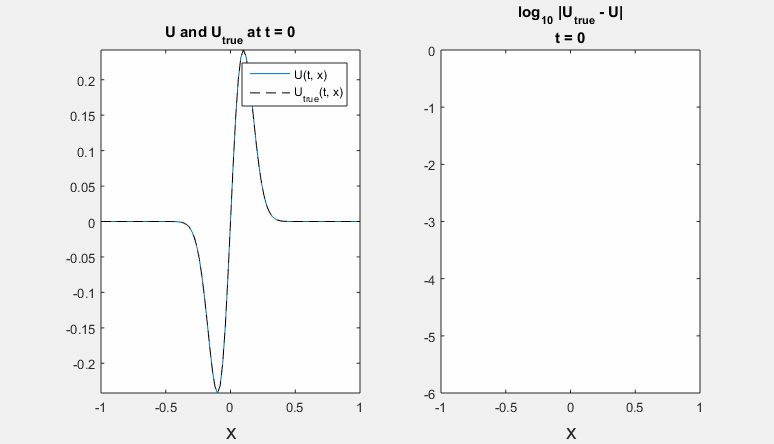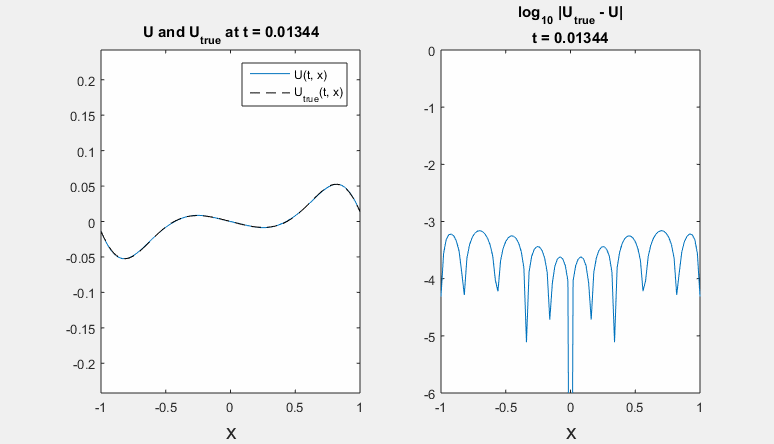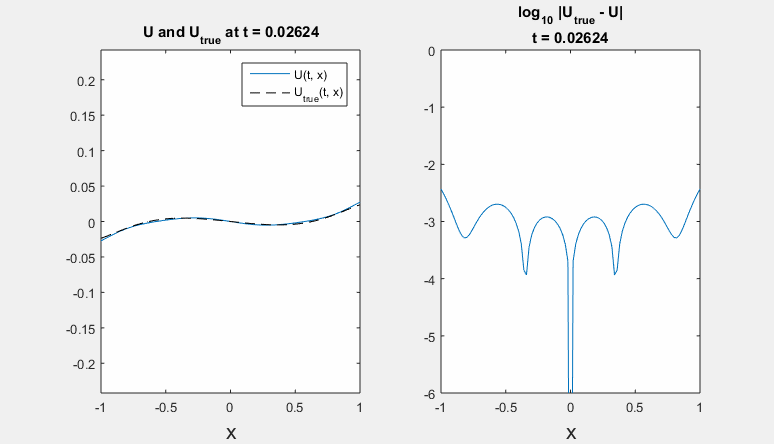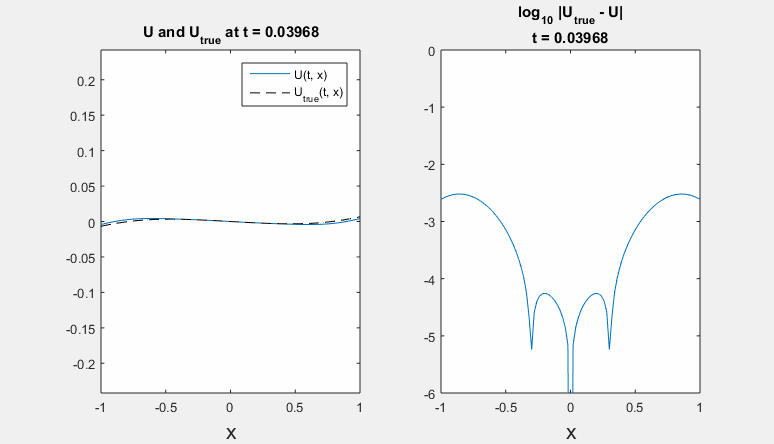
   Parameters: h = 0.02 m, tau = 0.00016 s., density  rho = 7860 kg / m^3, Young's modulus E = 210 * 10^9 Pa, radius R = 1,6 * 10^(-4) m. Left - refernce solution (calculated on an extended domain) and solution obtained using ICP boundary conditions; right - common logarithm of Chebyshev norm of difference between solutions.

   Polynomial degrees are equal for border and preborder points. Here we present results for degrees <7,6,6,8> and <4,5,8,8>.

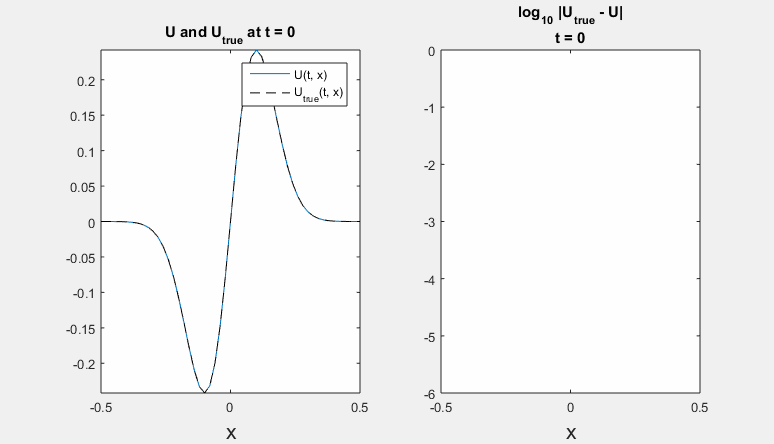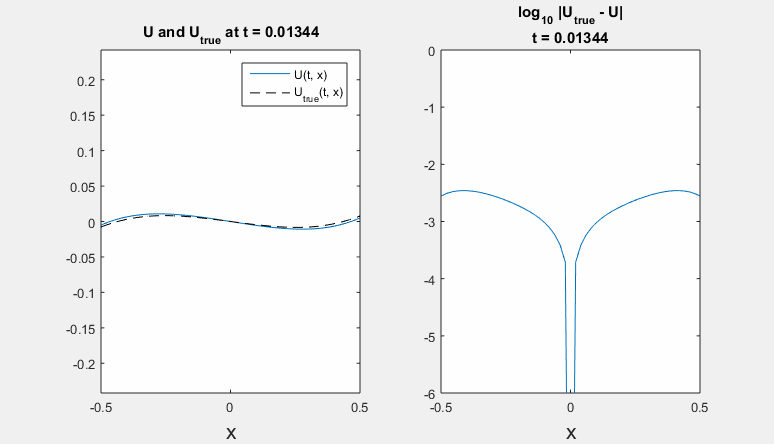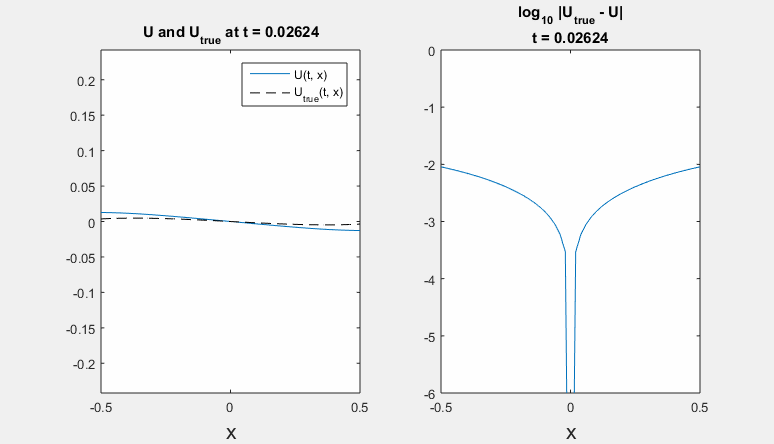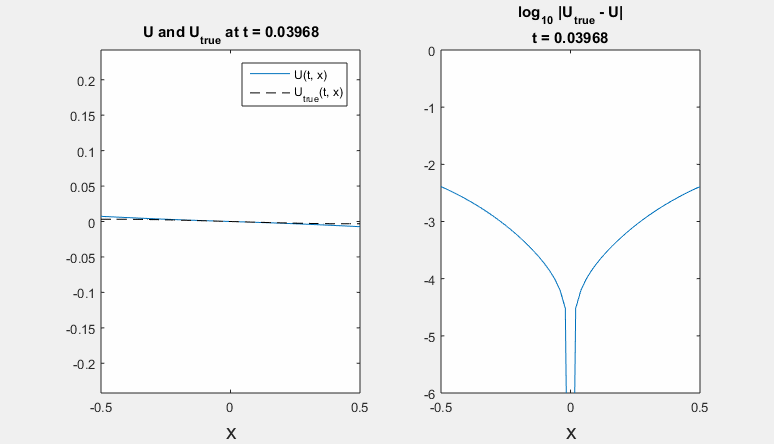
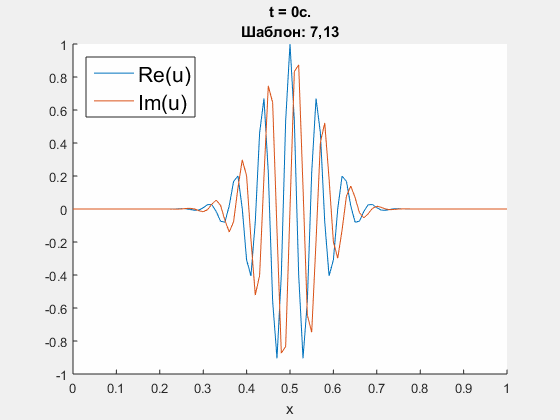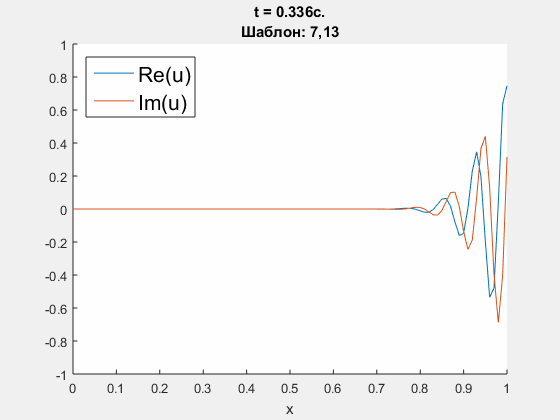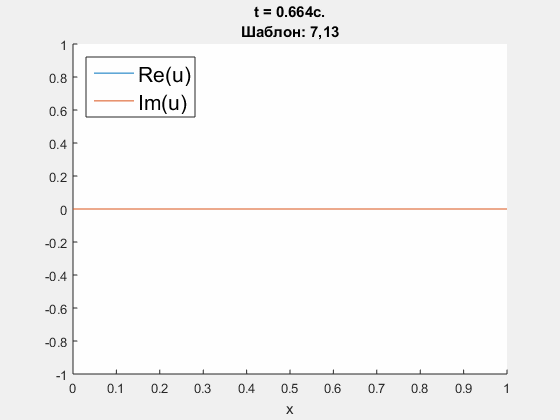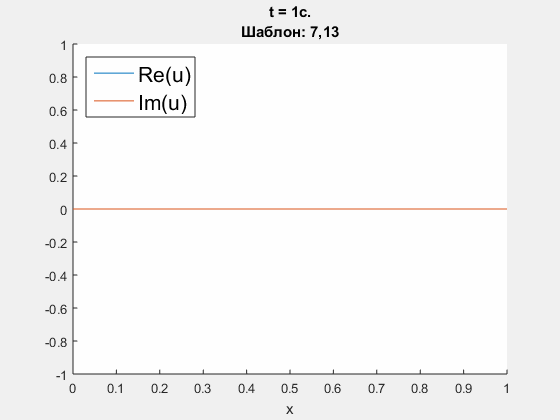
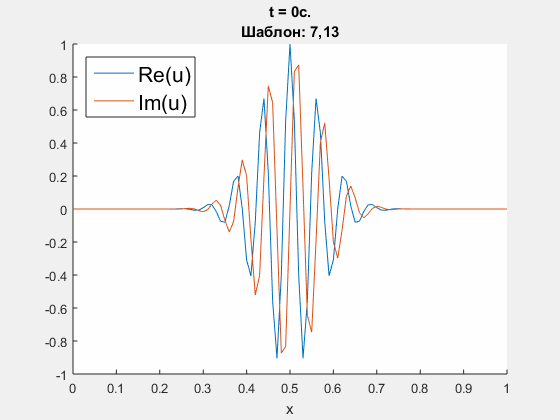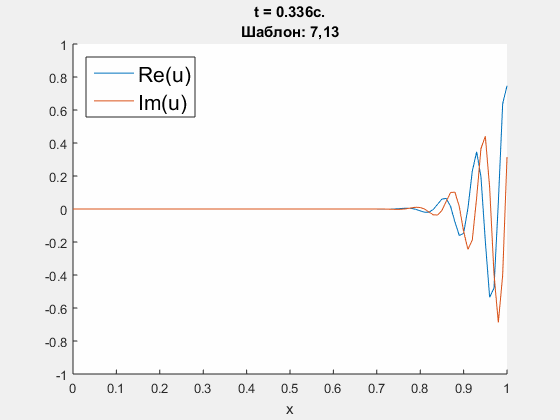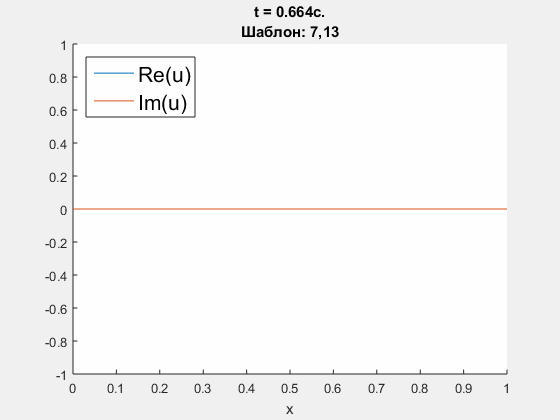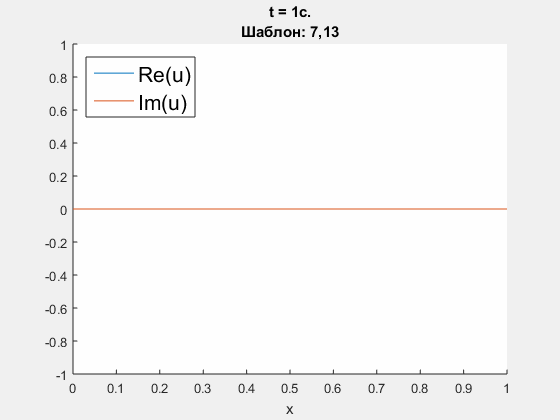
2. Crank - Nicolson approximation of Schrodinger equation.

   Initial condition is u(0, x) = exp(100i * (x-0.5) - (x-0.5)^2 / 100), which is supposed to go through the right border. ICP boundary conditions are constructed using polynomials' degrees <5, 10, 25>. Parameters: h = 0.01 m, tau = 0.004 s., dimensionless parameter nu = D * tau / h = 0.3i. Left - obtained solution, calculated using ICP boundary conditions; right - common logarith of Chebyshev norm of difference between obtained solution and refernce solution (calculated on an extended domain).

   
   

   

    

3. Wave equation, leap-frog scheme. Polynomial degrees are <3,1,3>.
   
   
   

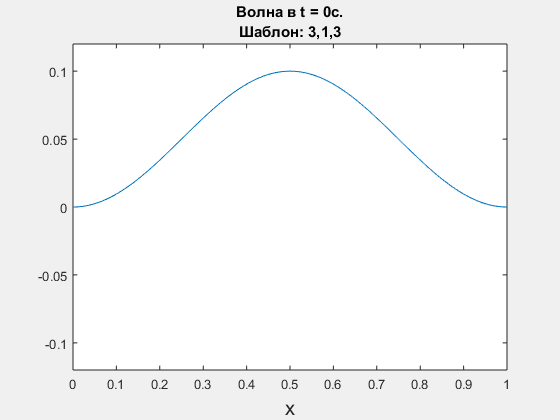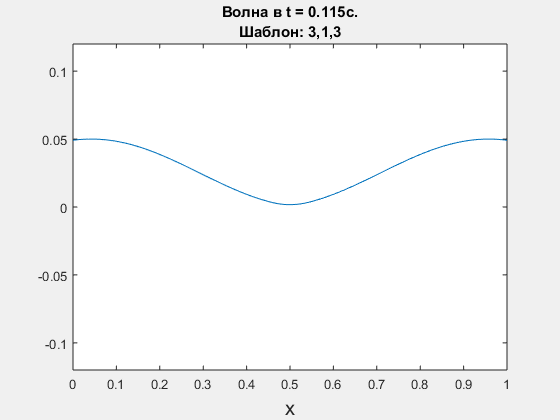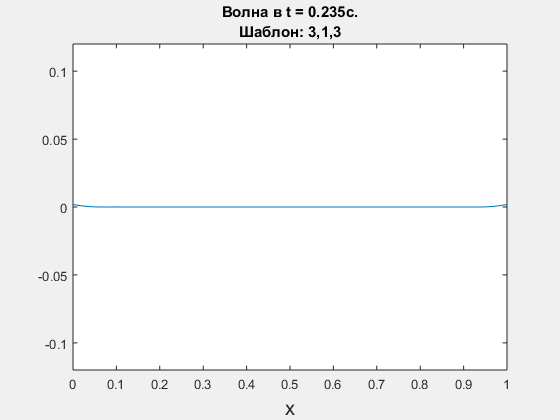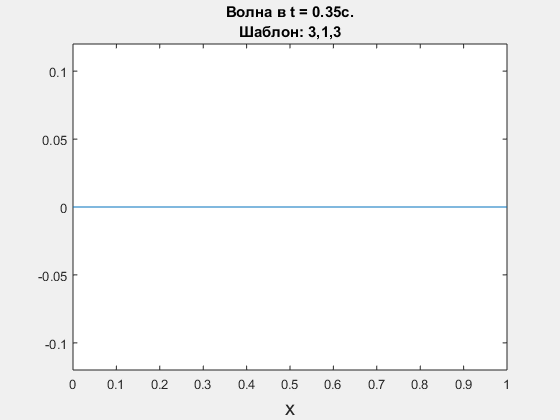
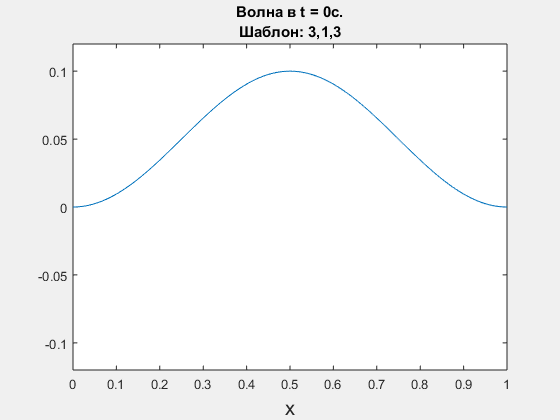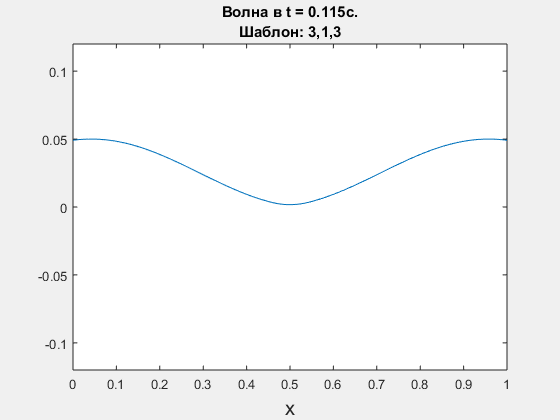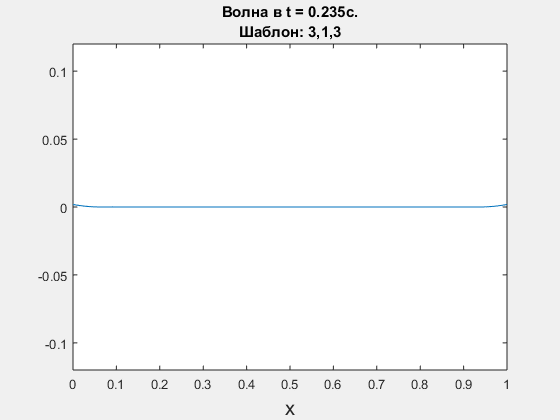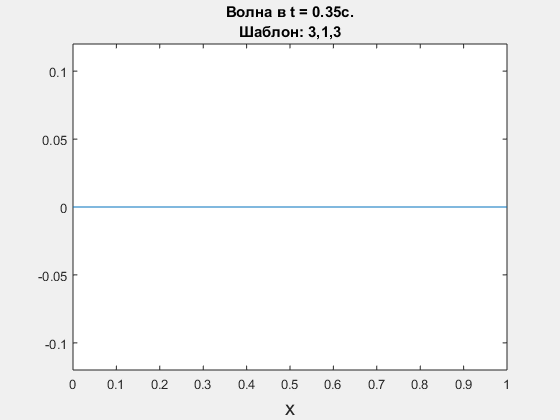
4. Diffusion equation, explicit Euler scheme. Polynomial degrees are <3,0,5>
   
   
   

   

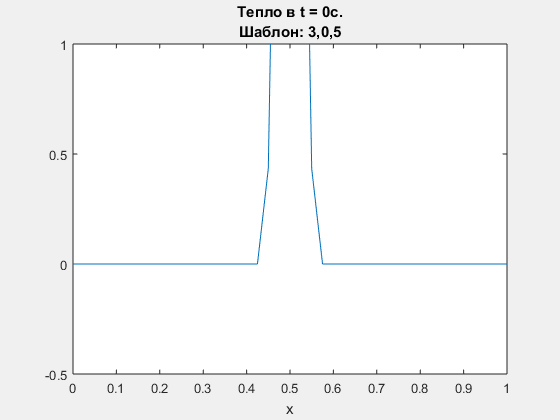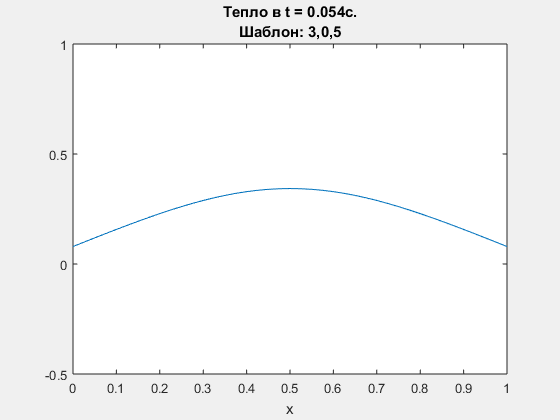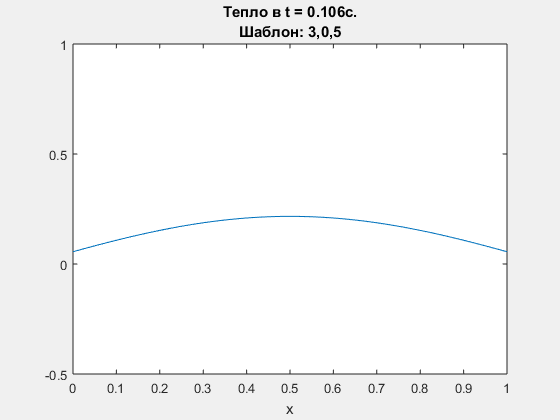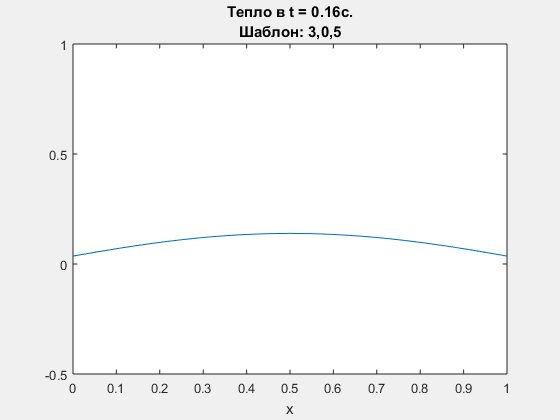
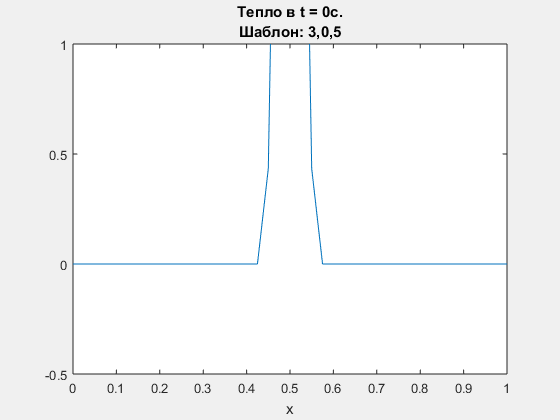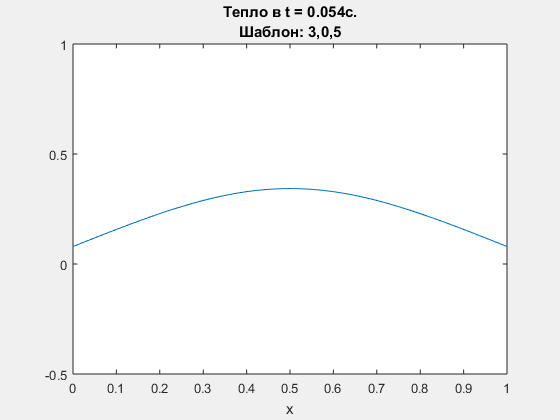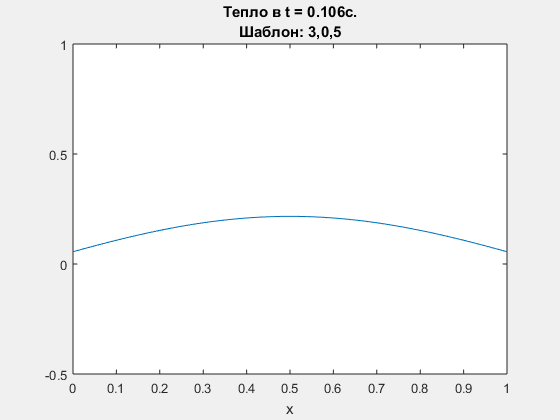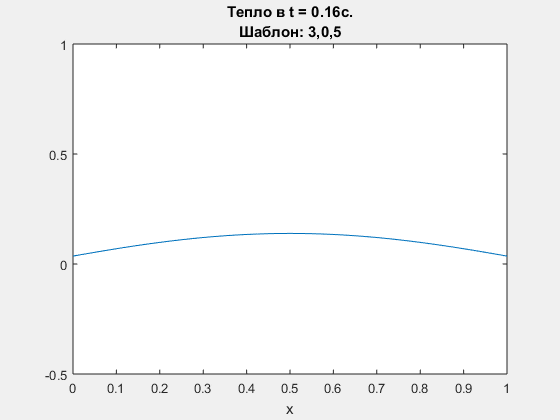
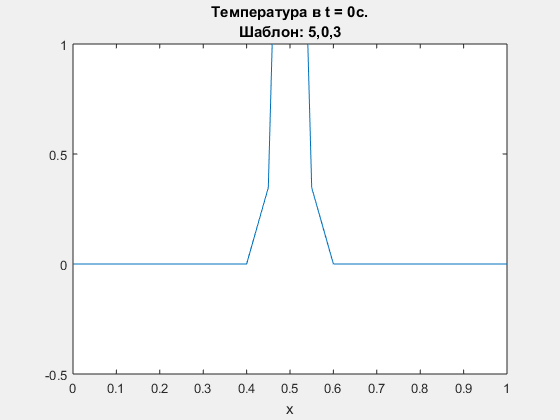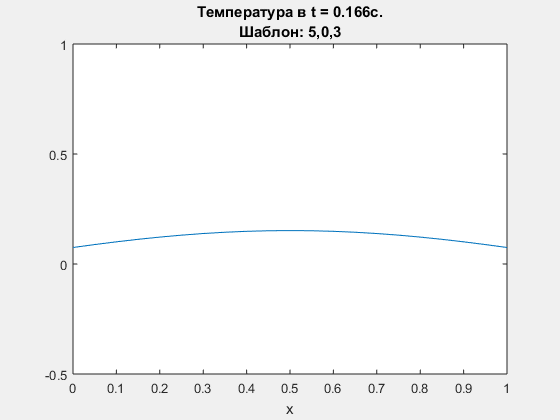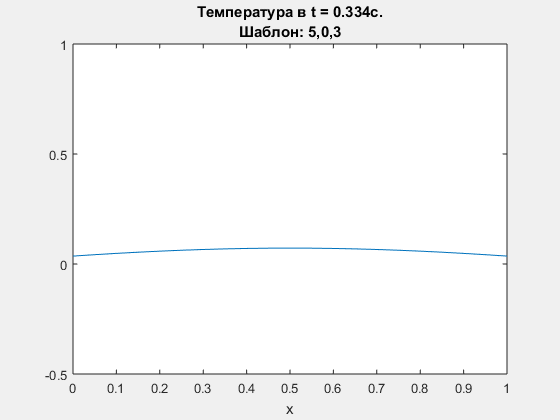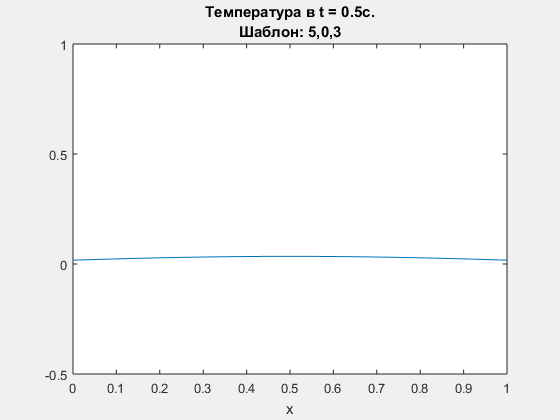
5. Diffusion equation, compacr scheme. Polynomial degrees are <5,0,3>.